Zero Knowledge Proofs Applications In Blockchain & Authentication.
As seen previously, (In Zero Knowledge Defition and Zero Knowledge Properties), the Zero Knowledge Proof method maintains the privacy of users, there is a range of applications where ZK can make a big impact.
About Blockchain
Providing pioneering solutions to the fundamentals of decentralization, Blockchain is one of the most disruptive technologies nowadays. Blockchain is a tamper-evident, shared digital ledger that records all transactions in public and private peer to peer networks[8].The ledger permanently records, and is spread across all the member nodes in a network. The records are contained within a sequential chain of cryptographic blocks, linked together by hashes. The way it works is: someone requests a transaction, this then is requested as a broadcast to a P2P network, made up of multiple notes, as discussed earlier. After the request is complete, these nodes will then validate the transaction by using known algorithms. Verified transactions can involve cryptocurrency, contracts or records, amongst others. Finally, once it’s verified, the transaction is combined with other transactions to create a new block of data, containing the information just verified. This block is then added to the existing set of blocks, called the blockchain, which is unalterable[8]. The transaction will be deemed as completed.
Prime Applications of Zero Knowledge Proof for blockchain
In today’s blockchain networks, the transactions are recorded in the public ledger, and by nature are transparent. Many blockchain networks use public databases. Technically, anyone that has access to the internet, can view the network’s transaction history. It is possible to gather the details associated with a transaction, as well as wallet details, but the name of the user will be unknown. Instead, it is likely to come across a public key, which is the unique code representing the user on the blockchain network. This public key is created via the cryptographic technique, safeguarding your privacy. However, as we just discussed it is possible to expose the history via other techniques. This makes blockchain anonymous, but doesn’t make it private in its entirety. Therefore, a user’s sensitive information stored in a blockchain is confidential, but not private. In this section, we describe possible solutions and applications that could solve the hindering of anonymity and privacy, of the wider use of blockchain, using Zero Knowledge Proofs. There are several use cases for ZK Proofs, in this paper we focus on authentication and the security for sensitive information.
Authentication
Zero Knowledge proof can also facilitate transmitting sensitive information, like authentication data, with better security. It can build a secure channel for the users to demonstrate their identity, by employing their information without revealing it. Avoiding data leakage.
Security for Sensitive Information
Zero Knowledge proof has the potential to revamp the way blockchain processes transactions. By adding a high-end security level to every block, which contains sensitive information, for example your bank credit card details, and the history. This extra layer of security could signify the ability for banks to only manipulate the required blocks, solely, when a user requests for information. Other blocks will remain untouched, adding the extra layer of protection to the process.
We have seen a couple of example use cases, however to see how we can secure these types of channels, in the next section, we’ll look at one of the foundational logarithms of Zero Proof.
Elliptic Curve Discrete Logarithm Problem
Algebraic groups built on top of elliptic curves together with the scalar multiplication, that is specified by a repeated addition. This can be used as a basic building block for asymmetric cryptography systems. Depending how tough the reversing scalar multiplication is of the operation, the stronger the system is. In order to understand how many times we have to multiply point G to get given point P, we would need to reverse this operation, which can be extremely expensive.
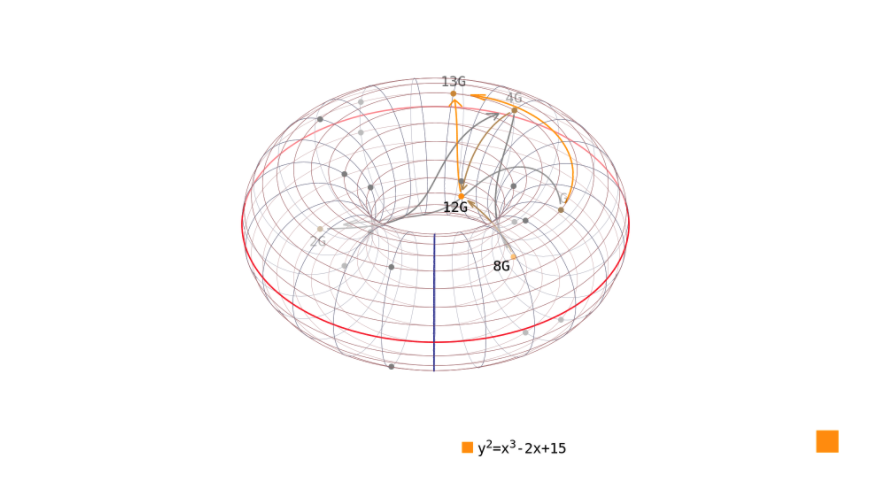Figure 2: Double Scalar Multiplication [12]
The method shown in Figure 2, depicts how this algorithm works. A known algorithm to find out how many times we have to multiply a given generator to obtain a given resulting point is to traverse the group of points on the elliptic curve, would be the naive algorithm, as seen in [13]. But for elliptic curves over finite fields, there won’t be enough rational points in the group, it would simply just take too long to perform such an operation. If we reverse in simple Weierstrass form [14], it is possible to obtain how many times it is needed to multiply a given point (e.g: g = [4,5] to obtain the operation’s resulting point, on the elliptic curve. Using this iterative approach, means that if we perform this for any number we are trying to find its respective points, the complexity will grow linearly with the number’s size .
Now that we have seen how ZK works, check out this Tutorial to see how you can implement Zero Knowledge for authentication and a final analysis.
References
[8]Bhardwaj, C., 2021. Blockchain: The Fundamentals of Decentralization {Infographic}. [online] Appinventiv. Available at: https://appinventiv.com/blog/basics-of-blockchain-infographic/ [Accessed 11 May 2021]. [9]Kurmi, J. and Sodhi, A., 2015. A Survey of Zero-Knowledge Proof for Authentication. International Journal of Advanced Research in Computer Science and Software Engineering, [online] 5(1). Available at: https://www.researchgate.net/publication/316492793_A_Survey_of_Zero-Knowledge_Proof_for_Authentication. [10] Archer, A., 2021. noknow. [online] PyPI. Available at: https://pypi.org/project/noknow/. [11]Archer, A., 2021. GoodiesHQ/noknow-python. [online] GitHub. Available at: https://github.com/GoodiesHQ/noknow-python. [12] Pantucek, D., 2018. Trustica » Elliptic curves: discrete logarithm problem. [online] Trustica.cz. Available at: https://trustica.cz/en/2018/05/10/elliptic-curves-discrete-logarithm-problem/. [13]Pantucek, D., 2018. Trustica » Elliptic curves: elliptic curves double and add. [online] Trustica.cz. Available at: https://trustica.cz/en/2018/05/03/elliptic-curves-double-and-add/. [14]Pantucek, D., 2018. Trustica » Elliptic curves: scalar multiplication revisited. [online] Trustica.cz. Available at: https://trustica.cz/en/2018/04/19/elliptic-curves-scalar-multiplication2/.
