Implementing ZK for authentication
Please check out:
- Zero Knowledge Defition and Zero Knowledge Properties, for understanding Zero Knowledge before this tutorial.
In this tutorial, we’ll be using Austin Archer’s python’s project: NoKnow.
NoKnow!
ZK is undoubtedly the future of privacy. In terms of authentication, theoretically speaking it is very promising, and can benefit greatly for various IT and application development industries. ZK allows organizations to guarantee secure AAA transactions and operations, meeting authentication, authorization and accounting, without exposing any private information. To demonstrate its potential, a more practical approach is needed. In this section, we experimented with NoKnow, a python library that implements Non-Interactive Zero-Knowledge Proof protocol, introduced in [10]. This library has been specifically designed for text-based secrets, like those seen in password authentication.
What is NoKnow?
Using -> Austin Archer’s python’s project: NoKnow.
This protocol is based on the fundamental problem of the Elliptic Curve Discrete Logarithm. In this principle, knowing a private variable n, is all that is required to produce a point in the curve. To do this, a signature is required, and will be the first step. The signature will be produced by multiplying a known value, like the hash of a password, by the elliptic curve generator point:
 Figure 2: Create signature function
Figure 2: Create signature function
Refer to Figure 2. The create_signature works by multiplying the secret’s hash (known value) times the curve point generator. As seen in line 152 of Figure 2. Now that this signature is produced, we can publish this signature publicly so that subsequent messages can be proven to have been produced by the same key/secret that created the signature. At the same time, the signature itself won’t reveal anything about the data that produced that calculation. Referring back to the previous section, note that in Non-Interactive ZK protocols, the proofs will be sent in a batch, rather than interactively share proof synchronously and repeatedly, with the verifier. Because credentials can now be verified against their signatures, one method of authentication is for the verifier, in this case, the server, to produce a random message, called token t[11]. This token can then be sent to the user with a request for them to produce proof with the provided token that can be verified against their public signature. From a security perspective, this is very valuable because it ensures that a single proof cannot be reused by a malicious actor in future authentication attempts. Checking the value of the signed data against what the server expects (the token) will add another extra layer of security, by making it harder for a malicious actor to generate a similar value. This token has to be large enough and randomised for this to take effect, that way the probabilities of someone replicating the request will be minimum. In this example, a static, randomised token approach is selected. It could be a consideration to use tokens with a short expiration. Please refer to Figure 3 below:
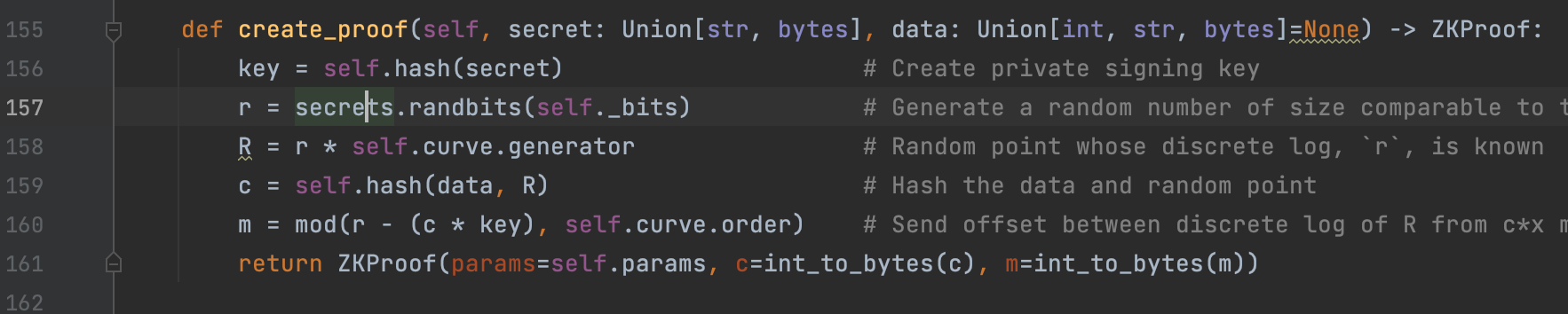 Figure 3: Create proof from token
Figure 3: Create proof from token
After the token is sent, the prover will generate the proof by going through the necessary calculations, in line 156, we see the private key is created by hashing the secret (password in our case)r is then created by randomising the secret value. We then generate a random point in the curve by multiplying by the hashed secret, we multiply by the randomised value, r. We now have proof generated, the next step will be to get it verified. Please refer to figure 4:
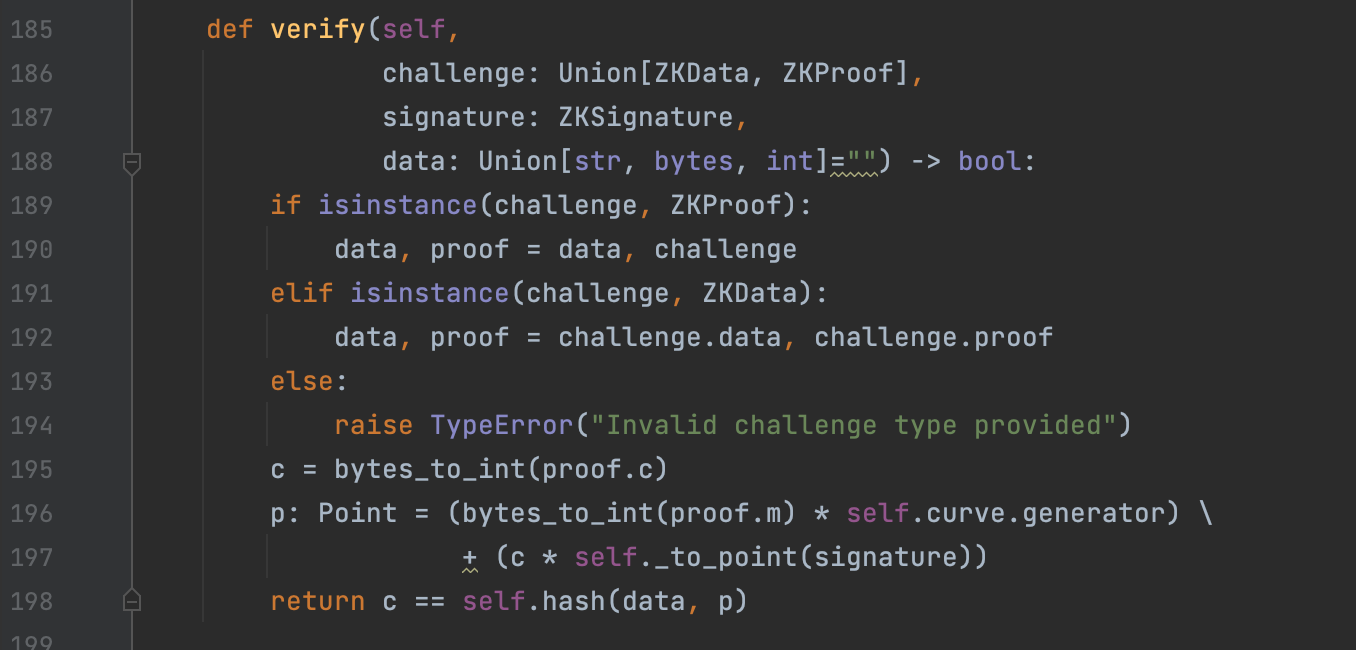 Figure 4: verify the proof During the validation step, what we are actually checking is against a hash. As seen in line 198, if c (generated proof in line 195) is equal to the hash of data and p (p being the point in the curve from the signature) then the verification will be valid. This check works, by following the basic principles of point multiplication with elliptic curves. Line 198 can then be translate to the following principle[12]:
Figure 4: verify the proof During the validation step, what we are actually checking is against a hash. As seen in line 198, if c (generated proof in line 195) is equal to the hash of data and p (p being the point in the curve from the signature) then the verification will be valid. This check works, by following the basic principles of point multiplication with elliptic curves. Line 198 can then be translate to the following principle[12]:
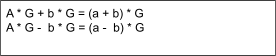
Where A * G + b * G represents var c in Figure 4 and (a+b) * G represents the hash of the data and p, or vice versa.
Evaluation: If this is so amazing, why aren’t we using it?
Challenges of Adopting Zero Knowledge in Practice
In this section, a number of challenges in the adoption of Zero Knowledge in practice is discussed.
Absence of standards
Zero Knowledge in itself is in the early stages, and it’s constantly evolving. At this time, there aren’t any standards, systems or languages that enable app developers and businesses to interact with the concept of ZK, for example, like API’s building blocks enabling businesses to integrate software and products into their workflow. Making it challenging to harness its potential.
Scalability
Since the algorithms that enable ZK require high computing capacity to operate at a high level, this is a challenge that restricts the adoption of ZK proof in blockchain environments, for example.
Designing Zero Knowledge Proof Systems
Designing ZK on a conceptual level, and formulating it’s semantic goal, can be achievable by a protocol designer. As it involves designing the requirements of a ZK system. But realising this semantic goal, can be quite difficult, unless you have extensive expertise in the field. This means that ZK is not accessible to a wider audience, making it really niche. Implementing it in practice, however, also comes with other challenges, like efficiency in the implementation process and the efficiency of code[15], as we saw in the shallow dive of NoKnow, in the implementation section, this project is also in an experimental state.
Efficiency of implementation process
Going from protocol specification to protocol implementation can be considered quite trivial, however in practice can introduce a lot of obstacles. Implementing and prototyping these kinds of protocols require a lot of manual and tedious tasks that can be error prone and can take several weeks. Another point to consider, as we discussed earlier, this is not something that is widely available, so it is often designed by cryptographers that have done extensive amounts of research in the field, but the implementation is done by engineers. This skill gap is also likely to bring more implementation errors[16].
Efficiency of Code
As we discussed in the Elliptic Curve Discrete Logarithm Problem, calculating the possible location points is very expensive. Efficient code means, in terms of computation time, memory usage, size of messages sent over a network etc Which in itself, is already quite hard to achieve.
Conclusion
In this tutorial we presented a view of the basics of Zero Knowledge, and possible applications for authentication with text based secrets, like passwords. Zero Knowledge proofs are probabilistic protocols, considering there could be a very small probability that allows cheating over the verification process. However, providing the ability to authenticate without having to reveal one’s password will make the system less vulnerable and introduces a stronger foundation of privacy. However, to translate the conceptualised and theoretical form of Zero Knowledge Proofs into practice, is still in a very experimental phase, and the challenges that come with it are still being evaluated. But with the potential Zero Knowledge Proof Systems withhold, this is a challenge that is likely to be overmatched.
References
[12] Pantucek, D., 2018. Trustica » Elliptic curves: discrete logarithm problem. [online] Trustica.cz. Available at: https://trustica.cz/en/2018/05/10/elliptic-curves-discrete-logarithm-problem/. [13]Pantucek, D., 2018. Trustica » Elliptic curves: elliptic curves double and add. [online] Trustica.cz. Available at: https://trustica.cz/en/2018/05/03/elliptic-curves-double-and-add/. [14]Pantucek, D., 2018. Trustica » Elliptic curves: scalar multiplication revisited. [online] Trustica.cz. Available at: https://trustica.cz/en/2018/04/19/elliptic-curves-scalar-multiplication2/. [15] J. Camenisch and E. V. Herreweghen. Design and implementation of the idemix anonymous credential system. In Proc. ACM CCS 2002, pages 21–30. ACM, 2002. http://www.zurich.ibm.com/security/idemix/ [16] J. Camenisch and A. Lysyanskaya. An efficient system for non-transferable anonymous credentials with optional anonymity revocation. In Advances in Cryptology – EUROCRYPT 2001, volume 2045, pages 93–118. Springer, 2001.
