Analysis Of Zero Knowledge Proof & Practical Applications
Introduction
A proof of a theorem can contain more knowledge than the fact the theorem might be true. When saying a statement of X is within Y, it is equivalent to saying there is a polynomial “proof system” for the existence of Y. This computational complexity theory of knowledge contained in a proof, was first introduced in [1] by Silvio M., Shafi G. and Charles R. in the 80s, and thus Zero Knowledge (ZK) was born. In this analysis, we evaluate the development of Zero Knowledge throughout the years, the challenges and benefits it brings, and showcase a prototyped design for the purpose of evaluating its value to current practices.
What is Zero Knowledge?
A zero knowledge, for proof of knowledge (ZK) is a two party protocol that enables the communication of a prover and a verifier. The prover should convince the verifier that it knows valuable, secret information that can satisfy the relation between both parties (proof of knowledge property), without the verifier able to learn the secret itself from the proof of knowledge (zero-knowledge property) [2]. Some protocols provide theoretical relevance, but lack efficiency for practical applications. However, there are reiterations of protocols that are relevant and plausible for real word use. These ZK protocols and techniques play an important role in applied cryptography. Various applications nowadays are oriented based on some of these techniques[3]. For example, identification schemes [4] and secure watermark detection [5], amongst others. A concrete practical set of protocols are presented to perform verifications, complementing ZK proof of knowledge.
How does it work?
It works by considering two different approaches where the deployment depends on the underlying applications: the first approach would allow to prove that the concealed information, the watermark, constitutes sufficient properties so that the prover can verify; the second approach allows both parties to jointly, securely and verifiably generate the information that has the necessary properties [5]. For the identification scheme approach, it uses a public-key signature based scheme in conjunction with an authentication scheme. In [4] it is demonstrated how this combination creates an algorithm that improves the speed of procedures, for the generation and verification of signatures, as well as the bit length of signatures.
Example Analysis & Protocols
The house analogy
We can understand ZK using an analogical life scenario, as follows:
A room can only be opened with a key, with nothing else available. The prover (P) would want to prove himself, owning the key that opens said room and without revealing the key to the verifier (to prevent leakage) that P can open said room, and in fact owns the key. If V determines a certain object contained within the room, and would be acceptable as proof, P could enter and take out said object. Or if it’s a very secret object, could describe it with characteristics only applicable for said object. This proof of knowledge represents zero-knowledge proof, where knowledge is the key[6]. The general process of Zero Knowledge Proof In reference to our previous analogy, we will follow the general process of using ZK, as seen in the following figure:
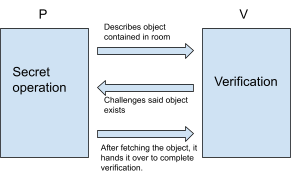
Figure 1: Analogical representation of ZK
As seen in figure 1, this process would be broken down as follows in ZK:
The prover P sends a promised random number “Q” to the verifier V. P executes a secret calculation of Q, and sends the result to V, as the second step, where it challenges the existence of the object, supposedly in the room. V verifies the calculation results sent by P. If the verification fails, the process is over. If it proves to be true, step 2) would be repeated N times, where every time the verification has to be successful, this way, the receipt of proof that V receives will increase in probability. This is translated to the analogy as P describing several other objects, and V asking P to keep fetching them and handing them over, to keep proving that P does have a key and can access the room.
In the next section, we describe the properties that make up the foundations of ZK. To go to the next section, click here
References
[1]GOLDWASSER, S., MICALI,, S. and RACKOFF, C., 2021. THE KNOWLEDGE COMPLEXITY OF INTERACTIVE PROOF SYSTEMS. [online] Citeseerx.ist.psu.edu. Available at: http://citeseerx.ist.psu.edu/viewdoc/download;jsessionid=185A41CC5695ECCD28256699E946F700?doi=10.1.1.397.4002&rep=rep1&type=pdf. [2] Bellare, M. and Goldreich, O., n.d. On Defining Proofs of Knowledge. Advances in Cryptology — CRYPTO’ 92, pp.390-420. [3]Bangerter, E., Barzan, S., Krenn, S., Sadeghi, A., Schneider, T. and Tsay, J., 2009. Bringing Zero-Knowledge Proofs of Knowledge to Practice. [online] pp.[1-12]. Available at: https://eprint.iacr.org/2009/211.pdf . [4]Schnorr, C., 1991. Efficient signature generation by smart cards. Journal of Cryptology, 4(3), pp.161-174. [5]Adelsbach, A., Rohe, M. & Sadeghi, AR. Complementing zero-knowledge watermark detection: Proving properties of embedded information without revealing it. Multimedia Systems 11, 143–158 (2005). https://doi.org/10.1007/s00530-005-0198-z [6] IJCSI International Journal of Computer Science Issues, 2013. Research on Zero-Knowledge Proof Protocol. [online] 10(1), pp.2-7. Available at: https://ijcsi.org/papers/IJCSI-10-1-1-194-200.pdf.
